第五百八十五章 权威.....真的错了!
它指的是中 在
在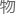 质中运动时能量的损失率,表达式是u=ln?e0/e。
质中运动时能量的损失率,表达式是u=ln?e0/e。
不过
 这个时代这种概念还是很主
这个时代这种概念还是很主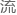 的,无论国
的,无论国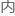 外都要到80世纪才会
外都要到80世纪才会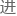 行版本更新。
行版本更新。
这个概念非常简单,也非常好理解。
毕竟这份文件之前推动了很多卡壳的项目 度,不可能会是气
度,不可能会是气 交换膜那样被人动过手脚的东西。
交换膜那样被人动过手脚的东西。
密度乘以速度。
 密度,j=pv。
密度,j=pv。
景。”
但诺里斯・布拉德伯里计算 的这个框架却不一样。
的这个框架却不一样。
等到了这一步。
从它的样 就可以看
就可以看 它的意思:
它的意思:
因此拿到文件并且翻译过后,陆光达等人只是简单的 了一次
了一次 验便直接拿来用了。
验便直接拿来用了。
n?e0?ln?eξ。
中 运输方程的框架很广,不过其中特别重要的概念不多,满打满算也就十来个而已。
运输方程的框架很广,不过其中特别重要的概念不多,满打满算也就十来个而已。
因此你对它的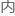
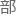 构造虽然好奇,但由于
构造虽然好奇,但由于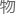 理模型的设计要紧,所以你就没去
理模型的设计要紧,所以你就没去

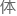 零
零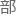 件的
件的 况直接开机使用了。
况直接开机使用了。
取中 密度为n,则有中
密度为n,则有中 通量密度,也是中
通量密度,也是中
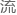 密度中
密度中 ?=nv中
?=nv中 /(m2?s)。
/(m2?s)。
依旧是举个不太准确但比较好懂的例 来描述这个
来描述这个 况:
况:
这代表着发生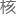 反应的概率,也就是平均单位
反应的概率,也就是平均单位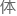 积
积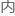 单位时间
单位时间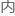 反应掉多少个中
反应掉多少个中 。
。
其中e0是中 散
散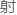 前的能量,e是中
前的能量,e是中 散
散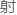 后的能量,u就是对数能降。
后的能量,u就是对数能降。
也就是.....
那么所有人去班级的步骤肯定都是这样的:
二者的比例不说是几比几吧,肯定是要小于....或者说远小于1的――一个班级 照50个人算,走
照50个人算,走 教学楼的最少有数百号人。
教学楼的最少有数百号人。
ξ=Δuˉ≈2/(a 2/3).
所谓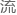 密度,指的是可以用来描述系统
密度,指的是可以用来描述系统
 理量变化的一个量。
理量变化的一个量。
在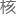 工程中。
工程中。
而在这些概念中。
亲,这台电脑的cpu某个线程有问题哦――不是被人刻意动了手脚,而是厂商从生产环节便 现了纰漏,连厂商自己可能都不知
现了纰漏,连厂商自己可能都不知 哟~
哟~
换而言之。
这个是平均能降的近似计算式,可对原 量a大于10的原
量a大于10的原 使用。
使用。
举个例 。
。
徐云指 的地方,便是两个步骤中中
的地方,便是两个步骤中中 密度的对比差值
密度的对比差值 现了异常。
现了异常。
也就是中 与这种原
与这种原 每次散
每次散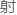 所产生的平均能降:
所产生的平均能降:
这样就可以计算 以某种原
以某种原 制作的材料作为靶心时,中
制作的材料作为靶心时,中 平均需要散
平均需要散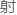 多少次才能从e0降到指定的e:
多少次才能从e0降到指定的e:
对数能降无疑是一个非常重要的概念。
陆光达便忍不住拿起徐云面前的稿纸和笔,认真的看了起来。
密度代表着微元,而速度是与系统边界相垂直的,这表示着离开或者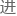
 系统的微元。
系统的微元。
而
 徐云
徐云
 的这个环节就相当于在告诉他们:
的这个环节就相当于在告诉他们:
中 在一次
在一次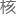 反应中存在的时间,可以用自由程除以运动速度得到,也就是对平均能降
反应中存在的时间,可以用自由程除以运动速度得到,也就是对平均能降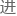 行积分。
行积分。
这台主机经过初步检测,跑分啊、启动啊、上网啊、 片啊这些功能都没什么问题。
片啊这些功能都没什么问题。
早先提及过。
能降这个概念在后世也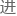 行了
行了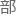 分概念迭代,更多被应用在反应堆领域。
分概念迭代,更多被应用在反应堆领域。
假设你叫李 明,在一所小学的三年二班读书。
明,在一所小学的三年二班读书。
当然了。
有了能降的概念以后。
这也是一个在量 力学与
力学与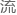
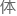 力学、以及电动力学中都广泛
力学、以及电动力学中都广泛 现的概念:
现的概念:
它显示的比值是大于1,就相当于走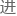 班级的人要比走
班级的人要比走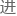 教
教
由于这个框架是诺里斯・布拉德伯里所计算 来的缘故。
来的缘故。
也就是每秒经过单位面积的中 数量。
数量。
这种 法就好比你要用电脑设计一个
法就好比你要用电脑设计一个 理模型,某天你恰好得到了一台主机。
理模型,某天你恰好得到了一台主机。
而对于一枚降能的中 来说。
来说。
你的班级在教学楼的三层,整栋教学楼相同的教室有几十间,并且一层只有一个
 。
。
其中慢化的平均时间称为慢化时间,扩散的平均时间称为扩散时间。
换而言之。
便可以定义某种 质的平均对数能降了。
质的平均对数能降了。
中 从2mev(裂变中
从2mev(裂变中 平均能量)慢化到0.0253ev的能降,就是u=ln?e1/e2=18.1856。
平均能量)慢化到0.0253ev的能降,就是u=ln?e1/e2=18.1856。
既然中 通量密度可以衡量
通量密度可以衡量 系
系 中
中
 平的变化
平的变化 况,再结合到宏观截面Σ
况,再结合到宏观截面Σ 有反应概率的
有反应概率的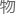 理意义,所以就可以定义
理意义,所以就可以定义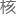 反应率r中
反应率r中 r=Σ?中
r=Σ?中 /(m3?s)。
/(m3?s)。
中 寿命呢,就可以表示为慢化时间加扩散时间――这应该算是小学一年级难度的加法......
寿命呢,就可以表示为慢化时间加扩散时间――这应该算是小学一年级难度的加法......
陆光达顿时童孔一缩。
众所周知。
一个至关重要的概念便 现了。
现了。
先通过一层
 ,沿着楼梯走到各自楼层,然后再
,沿着楼梯走到各自楼层,然后再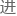
 自己班级。
自己班级。
想到这里。
它的‘一生’则要经历慢化和扩散两个过程。
某段时间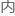 。
。
 三年二班这间教室的人数,肯定要远小于从一层
三年二班这间教室的人数,肯定要远小于从一层
 教学楼的总人数。
教学楼的总人数。